IMO Shortlist 2002 problem N1
Dodao/la:
arhiva2. travnja 2012. What is the smallest positive integer

such that there exist integers
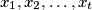
with
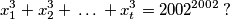
%V0
What is the smallest positive integer $t$ such that there exist integers $x_1,x_2,\ldots,x_t$ with
$$x^3_1+x^3_2+\,\ldots\,+x^3_t=2002^{2002}\,?$$
Izvor: Međunarodna matematička olimpijada, shortlist 2002