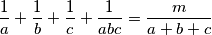
Is there a positive integer such that the equation has infinitely many solutions in positive integers ?
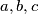
%V0
Is there a positive integer $m$ such that the equation $${1\over a}+{1\over b}+{1\over c}+{1\over abc}={m\over a+b+c}$$ has infinitely many solutions in positive integers $a,b,c$?
Izvor: Međunarodna matematička olimpijada, shortlist 2002
Školjka 
such that the equation 
has infinitely many solutions in positive integers 
?