IMO Shortlist 2003 problem A3
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0 Consider two monotonically decreasing sequences 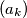 and
and  , where
, where 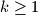 , and
, and 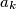 and
and 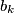 are positive real numbers for every k. Now, define the sequences
are positive real numbers for every k. Now, define the sequences
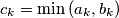 ;
;
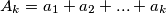 ;
;
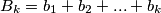 ;
;
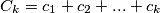
for all natural numbers k.
(a) Do there exist two monotonically decreasing sequences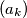 and
and  of positive real numbers such that the sequences
of positive real numbers such that the sequences 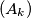 and
and 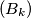 are not bounded, while the sequence
are not bounded, while the sequence 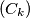 is bounded?
is bounded?
(b) Does the answer to problem (a) change if we stipulate that the sequence must be
must be 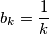 for all k ?
for all k ?
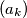 and
and  , where
, where 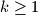 , and
, and 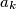 and
and 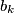 are positive real numbers for every k. Now, define the sequences
are positive real numbers for every k. Now, define the sequences 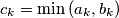 ;
; 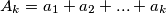 ;
; 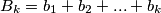 ;
; 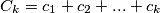
for all natural numbers k.
(a) Do there exist two monotonically decreasing sequences
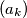 and
and  of positive real numbers such that the sequences
of positive real numbers such that the sequences 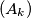 and
and 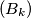 are not bounded, while the sequence
are not bounded, while the sequence 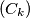 is bounded?
is bounded? (b) Does the answer to problem (a) change if we stipulate that the sequence
 must be
must be 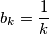 for all k ?
for all k ? Izvor: Međunarodna matematička olimpijada, shortlist 2003
 Školjka
Školjka 
