IMO Shortlist 2003 problem A5
Dodao/la:
arhiva2. travnja 2012. Let
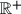
be the set of all positive real numbers. Find all functions
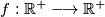
that satisfy the following conditions:
-
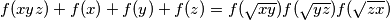
for all
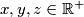
;
-
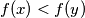
for all
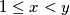
.
%V0
Let $\mathbb{R}^+$ be the set of all positive real numbers. Find all functions $f: \mathbb{R}^+ \longrightarrow \mathbb{R}^+$ that satisfy the following conditions:
- $f(xyz)+f(x)+f(y)+f(z)=f(\sqrt{xy})f(\sqrt{yz})f(\sqrt{zx})$ for all $x,y,z\in\mathbb{R}^+$;
- $f(x)<f(y)$ for all $1\le x<y$.
Izvor: Međunarodna matematička olimpijada, shortlist 2003