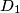
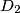
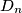
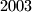
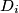
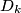
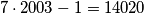
Let , , ..., be closed discs in the plane. (A closed disc is the region limited by a circle, taken jointly with this circle.) Suppose that every point in the plane is contained in at most discs . Prove that there exists a disc which intersects at most other discs .
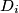
%V0
Let $D_1$, $D_2$, ..., $D_n$ be closed discs in the plane. (A closed disc is the region limited by a circle, taken jointly with this circle.) Suppose that every point in the plane is contained in at most $2003$ discs $D_i$. Prove that there exists a disc $D_k$ which intersects at most $7\cdot 2003 - 1 = 14020$ other discs $D_i$.
Izvor: Međunarodna matematička olimpijada, shortlist 2003
Školjka 
, 
, ..., 
be closed discs in the plane. (A closed disc is the region limited by a circle, taken jointly with this circle.) Suppose that every point in the plane is contained in at most 
discs 
. Prove that there exists a disc 
which intersects at most 
other discs