IMO Shortlist 2003 problem C4
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0 Given  real numbers
real numbers 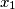 ,
, 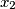 , ...,
, ..., 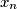 , and
, and  further real numbers
further real numbers 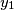 ,
, 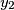 , ...,
, ..., 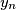 . The entries
. The entries 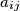 (with
(with 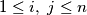 ) of an
) of an 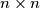 matrix
matrix  are defined as follows:
are defined as follows:
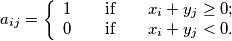
Further, let be an
be an 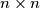 matrix whose elements are numbers from the set
matrix whose elements are numbers from the set 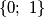 satisfying the following condition: The sum of all elements of each row of
satisfying the following condition: The sum of all elements of each row of  equals the sum of all elements of the corresponding row of
equals the sum of all elements of the corresponding row of  ; the sum of all elements of each column of
; the sum of all elements of each column of  equals the sum of all elements of the corresponding column of
equals the sum of all elements of the corresponding column of  . Show that in this case,
. Show that in this case, 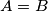 .
.
comment
(This one is from the ISL 2003, but in any case, the official problems and solutions - in German - are already online, hence I take the liberty to post it here.)
Darij
 real numbers
real numbers 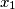 ,
, 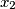 , ...,
, ..., 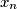 , and
, and  further real numbers
further real numbers 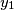 ,
, 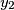 , ...,
, ..., 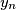 . The entries
. The entries 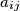 (with
(with 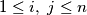 ) of an
) of an 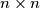 matrix
matrix  are defined as follows:
are defined as follows: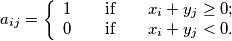
Further, let
 be an
be an 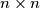 matrix whose elements are numbers from the set
matrix whose elements are numbers from the set 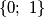 satisfying the following condition: The sum of all elements of each row of
satisfying the following condition: The sum of all elements of each row of  equals the sum of all elements of the corresponding row of
equals the sum of all elements of the corresponding row of  ; the sum of all elements of each column of
; the sum of all elements of each column of  equals the sum of all elements of the corresponding column of
equals the sum of all elements of the corresponding column of  . Show that in this case,
. Show that in this case, 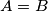 .
.comment
(This one is from the ISL 2003, but in any case, the official problems and solutions - in German - are already online, hence I take the liberty to post it here.)
Darij
Izvor: Međunarodna matematička olimpijada, shortlist 2003
 Školjka
Školjka 
