IMO Shortlist 2003 problem C6
Kvaliteta:
Avg: 0,0Težina:
Avg: 8,0 Let 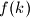 be the number of all non-negative integers
be the number of all non-negative integers  satisfying the following conditions:
satisfying the following conditions:
(1) The integer has exactly
has exactly  digits in the decimal representation (where the first digit is not necessarily non-zero!), i. e. we have
digits in the decimal representation (where the first digit is not necessarily non-zero!), i. e. we have 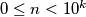 .
.
(2) These digits of n can be permuted in such a way that the resulting number is divisible by 11.
digits of n can be permuted in such a way that the resulting number is divisible by 11.
Show that for any positive integer number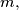 we have
we have 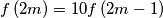 .
.
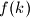 be the number of all non-negative integers
be the number of all non-negative integers  satisfying the following conditions:
satisfying the following conditions: (1) The integer
 has exactly
has exactly  digits in the decimal representation (where the first digit is not necessarily non-zero!), i. e. we have
digits in the decimal representation (where the first digit is not necessarily non-zero!), i. e. we have 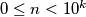 .
. (2) These
 digits of n can be permuted in such a way that the resulting number is divisible by 11.
digits of n can be permuted in such a way that the resulting number is divisible by 11. Show that for any positive integer number
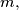 we have
we have 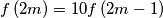 .
. Izvor: Međunarodna matematička olimpijada, shortlist 2003
 Školjka
Školjka 
