IMO Shortlist 2003 problem G5
Kvaliteta:
Avg: 4,0Težina:
Avg: 6,3 Let  be an isosceles triangle with
be an isosceles triangle with 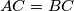 , whose incentre is
, whose incentre is  . Let
. Let  be a point on the circumcircle of the triangle
be a point on the circumcircle of the triangle 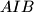 lying inside the triangle
lying inside the triangle  . The lines through
. The lines through  parallel to
parallel to  and
and 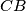 meet
meet  at
at  and
and  , respectively. The line through
, respectively. The line through  parallel to
parallel to  meets
meets  and
and 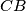 at
at  and
and  , respectively. Prove that the lines
, respectively. Prove that the lines 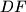 and
and 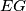 intersect on the circumcircle of the triangle
intersect on the circumcircle of the triangle  .
.
comment
(According to my team leader, last year some of the countries wanted a geometry question that was even easier than this...that explains IMO 2003/4...)
[Note by Darij: This was also Problem 6 of the German pre-TST 2004, written in December 03.]
Edited by Orl.
 be an isosceles triangle with
be an isosceles triangle with 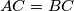 , whose incentre is
, whose incentre is  . Let
. Let  be a point on the circumcircle of the triangle
be a point on the circumcircle of the triangle 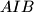 lying inside the triangle
lying inside the triangle  . The lines through
. The lines through  parallel to
parallel to  and
and 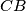 meet
meet  at
at  and
and  , respectively. The line through
, respectively. The line through  parallel to
parallel to  meets
meets  and
and 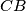 at
at  and
and  , respectively. Prove that the lines
, respectively. Prove that the lines 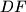 and
and 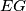 intersect on the circumcircle of the triangle
intersect on the circumcircle of the triangle  .
. comment
(According to my team leader, last year some of the countries wanted a geometry question that was even easier than this...that explains IMO 2003/4...)
[Note by Darij: This was also Problem 6 of the German pre-TST 2004, written in December 03.]
Edited by Orl.
Izvor: Međunarodna matematička olimpijada, shortlist 2003
 Školjka
Školjka 
