IMO Shortlist 2003 problem N8
Kvaliteta:
Avg: 0,0Težina:
Avg: 9,0 Let  be a prime number and let
be a prime number and let  be a set of positive integers that satisfies the following conditions: (1) the set of prime divisors of the elements in
be a set of positive integers that satisfies the following conditions: (1) the set of prime divisors of the elements in  consists of
consists of 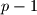 elements; (2) for any nonempty subset of
elements; (2) for any nonempty subset of  , the product of its elements is not a perfect
, the product of its elements is not a perfect  -th power. What is the largest possible number of elements in
-th power. What is the largest possible number of elements in  ?
?
 be a prime number and let
be a prime number and let  be a set of positive integers that satisfies the following conditions: (1) the set of prime divisors of the elements in
be a set of positive integers that satisfies the following conditions: (1) the set of prime divisors of the elements in  consists of
consists of 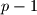 elements; (2) for any nonempty subset of
elements; (2) for any nonempty subset of  , the product of its elements is not a perfect
, the product of its elements is not a perfect  -th power. What is the largest possible number of elements in
-th power. What is the largest possible number of elements in  ?
? Izvor: Međunarodna matematička olimpijada, shortlist 2003
 Školjka
Školjka 
