IMO Shortlist 2004 problem C2
Kvaliteta:
Avg: 4,0Težina:
Avg: 6,0 Let 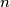 and
and  be positive integers. There are given
be positive integers. There are given 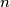 circles in the plane. Every two of them intersect at two distinct points, and all points of intersection they determine are pairwisely distinct (i. e. no three circles have a common point). No three circles have a point in common. Each intersection point must be colored with one of
circles in the plane. Every two of them intersect at two distinct points, and all points of intersection they determine are pairwisely distinct (i. e. no three circles have a common point). No three circles have a point in common. Each intersection point must be colored with one of  distinct colors so that each color is used at least once and exactly
distinct colors so that each color is used at least once and exactly  distinct colors occur on each circle. Find all values of
distinct colors occur on each circle. Find all values of 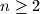 and
and  for which such a coloring is possible.
for which such a coloring is possible.
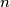 and
and  be positive integers. There are given
be positive integers. There are given 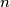 circles in the plane. Every two of them intersect at two distinct points, and all points of intersection they determine are pairwisely distinct (i. e. no three circles have a common point). No three circles have a point in common. Each intersection point must be colored with one of
circles in the plane. Every two of them intersect at two distinct points, and all points of intersection they determine are pairwisely distinct (i. e. no three circles have a common point). No three circles have a point in common. Each intersection point must be colored with one of  distinct colors so that each color is used at least once and exactly
distinct colors so that each color is used at least once and exactly  distinct colors occur on each circle. Find all values of
distinct colors occur on each circle. Find all values of 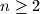 and
and  for which such a coloring is possible.
for which such a coloring is possible. Izvor: Međunarodna matematička olimpijada, shortlist 2004
 Školjka
Školjka 
