IMO Shortlist 2004 problem C3
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0 In a country there are 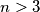 cities. We can add a street between
cities. We can add a street between  cities
cities  and
and  , iff there exist
, iff there exist  cities
cities  and
and  different from
different from  and
and  such that there is no street between
such that there is no street between  and
and  ,
,  and
and  , and
, and  and
and  . Find the biggest number of streets one can construct!
. Find the biggest number of streets one can construct!
Official Wording The following operation is allowed on a finite graph: Choose an arbitrary cycle of length 4 (if there is any), choose an arbitrary edge in that cycle, and delete it from the graph. For a fixed integer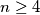 , find the least number of edges of a graph that can be obtained by repeated applications of this operation from the complete graph on
, find the least number of edges of a graph that can be obtained by repeated applications of this operation from the complete graph on  vertices (where each pair of vertices are joined by an edge).
vertices (where each pair of vertices are joined by an edge).
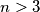 cities. We can add a street between
cities. We can add a street between  cities
cities  and
and  , iff there exist
, iff there exist  cities
cities  and
and  different from
different from  and
and  such that there is no street between
such that there is no street between  and
and  ,
,  and
and  , and
, and  and
and  . Find the biggest number of streets one can construct!
. Find the biggest number of streets one can construct! Official Wording The following operation is allowed on a finite graph: Choose an arbitrary cycle of length 4 (if there is any), choose an arbitrary edge in that cycle, and delete it from the graph. For a fixed integer
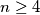 , find the least number of edges of a graph that can be obtained by repeated applications of this operation from the complete graph on
, find the least number of edges of a graph that can be obtained by repeated applications of this operation from the complete graph on  vertices (where each pair of vertices are joined by an edge).
vertices (where each pair of vertices are joined by an edge). Izvor: Međunarodna matematička olimpijada, shortlist 2004
 Školjka
Školjka 
