IMO Shortlist 2004 problem C6
Dodao/la:
arhiva2. travnja 2012. For an
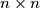
matrix

, let
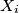
be the set of entries in row

, and
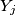
the set of entries in column

,
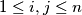
. We say that

is golden if
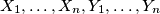
are distinct sets. Find the least integer

such that there exists a
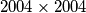
golden matrix with entries in the set
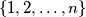
.
%V0
For an ${n\times n}$ matrix $A$, let $X_{i}$ be the set of entries in row $i$, and $Y_{j}$ the set of entries in column $j$, ${1\leq i,j\leq n}$. We say that $A$ is golden if ${X_{1},\dots ,X_{n},Y_{1},\dots ,Y_{n}}$ are distinct sets. Find the least integer $n$ such that there exists a ${2004\times 2004}$ golden matrix with entries in the set ${\{1,2,\dots ,n\}}$.
Izvor: Međunarodna matematička olimpijada, shortlist 2004