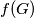
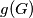
For a finite graph , let be the number of triangles and the number of tetrahedra formed by edges of . Find the least constant such that
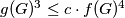
for every graph .
%V0
For a finite graph $G$, let $f(G)$ be the number of triangles and $g(G)$ the number of tetrahedra formed by edges of $G$. Find the least constant $c$ such that
$g(G)^3 \leq c\cdot f(G)^4$
for every graph $G$.
Izvor: Međunarodna matematička olimpijada, shortlist 2004
Školjka 
, let 
be the number of triangles and 
the number of tetrahedra formed by edges of 
such that 