IMO Shortlist 2004 problem G5
Dodao/la:
arhiva2. travnja 2012. Let
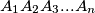
be a regular n-gon. Let

and
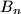
be the midpoints of its sides
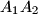
and
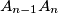
. Also, for every
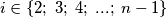
, let

be the point of intersection of the lines
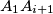
and
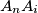
, and let
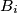
be the point of intersection of the angle bisector bisector of the angle
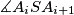
with the segment
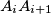
.
Prove that:
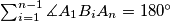
.
%V0
Let $A_1A_2A_3...A_n$ be a regular n-gon. Let $B_1$ and $B_n$ be the midpoints of its sides $A_1A_2$ and $A_{n-1}A_n$. Also, for every $i\in\left\{2;\;3;\;4;\;...;\;n-1\right\}$, let $S$ be the point of intersection of the lines $A_1A_{i+1}$ and $A_nA_i$, and let $B_i$ be the point of intersection of the angle bisector bisector of the angle $\measuredangle A_iSA_{i+1}$ with the segment $A_iA_{i+1}$.
Prove that: $\sum_{i=1}^{n-1} \measuredangle A_1B_iA_n=180^{\circ}$.
Izvor: Međunarodna matematička olimpijada, shortlist 2004