IMO Shortlist 2004 problem G6
Kvaliteta:
Avg: 0,0Težina:
Avg: 8,0 Let  be a convex polygon. Prove that there exists a convex hexagon that is contained in
be a convex polygon. Prove that there exists a convex hexagon that is contained in  and whose area is at least
and whose area is at least  of the area of the polygon
of the area of the polygon  .
.
Alternative version. Let be a convex polygon with
be a convex polygon with 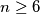 vertices. Prove that there exists a convex hexagon with
vertices. Prove that there exists a convex hexagon with
a) vertices on the sides of the polygon (or)
b) vertices among the vertices of the polygon
such that the area of the hexagon is at least of the area of the polygon.
of the area of the polygon.
I couldn't solve this one, partially because I'm not quite sure of the statements' meaning (a) or (b) :)
Obviously if a) is true then so is b).
 be a convex polygon. Prove that there exists a convex hexagon that is contained in
be a convex polygon. Prove that there exists a convex hexagon that is contained in  and whose area is at least
and whose area is at least  of the area of the polygon
of the area of the polygon  .
. Alternative version. Let
 be a convex polygon with
be a convex polygon with 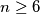 vertices. Prove that there exists a convex hexagon with
vertices. Prove that there exists a convex hexagon with a) vertices on the sides of the polygon (or)
b) vertices among the vertices of the polygon
such that the area of the hexagon is at least
 of the area of the polygon.
of the area of the polygon. I couldn't solve this one, partially because I'm not quite sure of the statements' meaning (a) or (b) :)
Obviously if a) is true then so is b).
Izvor: Međunarodna matematička olimpijada, shortlist 2004
 Školjka
Školjka 
