IMO Shortlist 2004 problem G8
Dodao/la:
arhiva2. travnja 2012. Given a cyclic quadrilateral

, let

be the midpoint of the side

, and let

be a point on the circumcircle of triangle
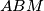
. Assume that the point

is different from the point

and satisfies
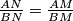
. Prove that the points

,

,

are collinear, where
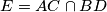
and
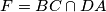
.
%V0
Given a cyclic quadrilateral $ABCD$, let $M$ be the midpoint of the side $CD$, and let $N$ be a point on the circumcircle of triangle $ABM$. Assume that the point $N$ is different from the point $M$ and satisfies $\frac{AN}{BN}=\frac{AM}{BM}$. Prove that the points $E$, $F$, $N$ are collinear, where $E=AC\cap BD$ and $F=BC\cap DA$.
Izvor: Međunarodna matematička olimpijada, shortlist 2004