IMO Shortlist 2004 problem N4
Dodao/la:
arhiva2. travnja 2012. Let

be a fixed integer greater than 1, and let
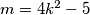
. Show that there exist positive integers

and

such that the sequence
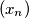
defined by
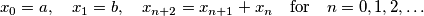
has all of its terms relatively prime to

.
%V0
Let $k$ be a fixed integer greater than 1, and let ${m=4k^2-5}$. Show that there exist positive integers $a$ and $b$ such that the sequence $(x_n)$ defined by $$x_0=a,\quad x_1=b,\quad x_{n+2}=x_{n+1}+x_n\quad\text{for}\quad n=0,1,2,\dots$$ has all of its terms relatively prime to $m$.
Izvor: Međunarodna matematička olimpijada, shortlist 2004