IMO Shortlist 2005 problem A1
Dodao/la:
arhiva2. travnja 2012. Find all pairs of integers
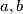
for which there exists a polynomial
![P(x) \in \mathbb{Z}[X]](/media/m/c/8/8/c88440085030c32a41066167316e5adc.png)
such that product
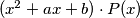
is a polynomial of a form
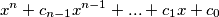
where each of
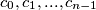
is equal to

or
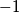
.
%V0
Find all pairs of integers $a,b$ for which there exists a polynomial $P(x) \in \mathbb{Z}[X]$ such that product $(x^2+ax+b)\cdot P(x)$ is a polynomial of a form $$x^n+c_{n-1}x^{n-1}+...+c_1x+c_0$$ where each of $c_0,c_1,...,c_{n-1}$ is equal to $1$ or $-1$.
Izvor: Međunarodna matematička olimpijada, shortlist 2005