IMO Shortlist 2005 problem A3
Dodao/la:
arhiva2. travnja 2012. Four real numbers

,

,

,

satisfy
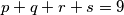
and
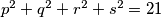
. Prove that there exists a permutation
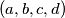
of
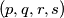
such that
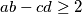
.
%V0
Four real numbers $p$, $q$, $r$, $s$ satisfy $p+q+r+s = 9$ and $p^{2}+q^{2}+r^{2}+s^{2}= 21$. Prove that there exists a permutation $\left(a,b,c,d\right)$ of $\left(p,q,r,s\right)$ such that $ab-cd \geq 2$.
Izvor: Međunarodna matematička olimpijada, shortlist 2005