IMO Shortlist 2005 problem C2
Kvaliteta:
Avg: 4,0Težina:
Avg: 6,0 This ISL 2005 problem has not been used in any TST I know. A pity, since it is a nice problem, but in its shortlist formulation, it is absolutely incomprehensible. Here is a mathematical restatement of the problem:
Let be a nonnegative integer.
be a nonnegative integer.
A forest consists of rooted (i. e. oriented) trees. Each vertex of the forest is either a leaf or has two successors. A vertex is called an extended successor of a vertex
is called an extended successor of a vertex 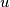 if there is a chain of vertices
if there is a chain of vertices 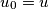 ,
, 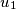 ,
, 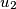 , ...,
, ..., 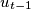 ,
, 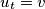 with
with 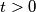 such that the vertex
such that the vertex 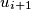 is a successor of the vertex
is a successor of the vertex 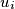 for every integer
for every integer  with
with 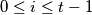 . A vertex is called dynastic if it has two successors and each of these successors has at least
. A vertex is called dynastic if it has two successors and each of these successors has at least  extended successors.
extended successors.
Prove that if the forest has vertices, then there are at most
vertices, then there are at most 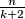 dynastic vertices.
dynastic vertices.
Let
 be a nonnegative integer.
be a nonnegative integer.A forest consists of rooted (i. e. oriented) trees. Each vertex of the forest is either a leaf or has two successors. A vertex
 is called an extended successor of a vertex
is called an extended successor of a vertex 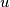 if there is a chain of vertices
if there is a chain of vertices 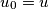 ,
, 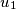 ,
, 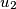 , ...,
, ..., 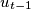 ,
, 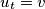 with
with 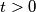 such that the vertex
such that the vertex 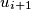 is a successor of the vertex
is a successor of the vertex 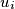 for every integer
for every integer  with
with 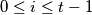 . A vertex is called dynastic if it has two successors and each of these successors has at least
. A vertex is called dynastic if it has two successors and each of these successors has at least  extended successors.
extended successors.Prove that if the forest has
 vertices, then there are at most
vertices, then there are at most 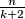 dynastic vertices.
dynastic vertices. Izvor: Međunarodna matematička olimpijada, shortlist 2005
 Školjka
Školjka 
