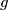
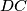
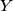
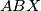
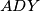
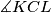
Let be a parallelogram. A variable line through the vertex intersects the rays and at the points and , respectively. Let and be the -excenters of the triangles and . Show that the angle is independent of the line .
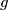
%V0
Let $ABCD$ be a parallelogram. A variable line $g$ through the vertex $A$ intersects the rays $BC$ and $DC$ at the points $X$ and $Y$, respectively. Let $K$ and $L$ be the $A$-excenters of the triangles $ABX$ and $ADY$. Show that the angle $\measuredangle KCL$ is independent of the line $g$.
Izvor: Međunarodna matematička olimpijada, shortlist 2005
Školjka 
be a parallelogram. A variable line 
through the vertex 
intersects the rays 
and 
at the points 
and 
, respectively. Let 
and 
be the 
and 
. Show that the angle 
is independent of the line