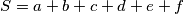
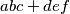
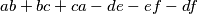
Let , , , , , be positive integers and let . Suppose that the number divides and . Prove that is composite.
%V0
Let $a$, $b$, $c$, $d$, $e$, $f$ be positive integers and let $S = a+b+c+d+e+f$.
Suppose that the number $S$ divides $abc+def$ and $ab+bc+ca-de-ef-df$. Prove that $S$ is composite.
Izvor: Međunarodna matematička olimpijada, shortlist 2005
Školjka 
, 
, 
, 
, 
, 
be positive integers and let 
. 
divides 
and 
. Prove that