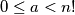
Find all positive integers such that there exists a unique integer such that with the following property:
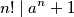
%V0
Find all positive integers $n$ such that there exists a unique integer $a$ such that $0\leq a < n!$ with the following property:
$$n!\mid a^n + 1$$
Izvor: Međunarodna matematička olimpijada, shortlist 2005
Školjka 
such that there exists a unique integer 
such that 
with the following property: 