IMO Shortlist 2006 problem A1
Dodao/la:
arhiva2. travnja 2012. 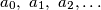
is a sequence of real numbers such that
![a_{n + 1} = \left[a_{n}\right]\cdot \left\{a_{n}\right\}](/media/m/8/4/1/841a9a2ad06c20187088b2f582b7c6d1.png)
prove that exist
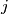
such that for every
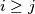
we have
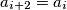
.
%V0
$a_{0},\ a_{1},\ a_{2},\dots$ is a sequence of real numbers such that
$$a_{n + 1} = \left[a_{n}\right]\cdot \left\{a_{n}\right\}$$
prove that exist $j$ such that for every $i\geq j$ we have $a_{i + 2} = a_{i}$.
Izvor: Međunarodna matematička olimpijada, shortlist 2006