IMO Shortlist 2006 problem A4
Dodao/la:
arhiva2. travnja 2012. Prove the inequality:
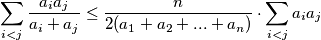
for positive reals
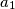
,
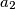
, ...,
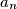
.
%V0
Prove the inequality:
$\displaystyle \sum_{i < j}{\frac {a_{i}a_{j}}{a_{i} + a_{j}}}\leq \frac {n}{2(a_{1} + a_{2} + ... + a_{n})}\cdot \sum_{i < j}{a_{i}a_{j}}$
for positive reals $a_{1}$, $a_{2}$, ..., $a_{n}$.
Izvor: Međunarodna matematička olimpijada, shortlist 2006