IMO Shortlist 2006 problem G4
Dodao/la:
arhiva2. travnja 2012. Let

be a triangle such that
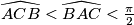
. Let

be a point of
![[AC]](/media/m/c/7/4/c741f6e67c75b27db5e363fbcf5393c6.png)
such that
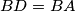
. The incircle of

touches
![[AB]](/media/m/1/0/6/10652e809a6cb10509d19772365232e2.png)
at

and
![[AC]](/media/m/c/7/4/c741f6e67c75b27db5e363fbcf5393c6.png)
at

. Let
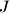
be the center of the incircle of
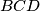
. Prove that
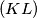
intersects
![[AJ]](/media/m/4/d/3/4d35637bd1d22b6a0da26de27970690f.png)
at its middle.
%V0
Let $ABC$ be a triangle such that $\widehat{ACB} < \widehat{BAC} < \frac {\pi}{2}$. Let $D$ be a point of $[AC]$ such that $BD = BA$. The incircle of $ABC$ touches $[AB]$ at $K$ and $[AC]$ at $L$. Let $J$ be the center of the incircle of $BCD$. Prove that $(KL)$ intersects $[AJ]$ at its middle.
Izvor: Međunarodna matematička olimpijada, shortlist 2006