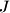
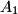
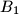
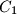
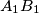
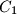
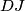
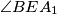
In triangle , let be the center of the excircle tangent to side at and to the extensions of the sides and at and respectively. Suppose that the lines and are perpendicular and intersect at . Let be the foot of the perpendicular from to line . Determine the angles and .
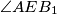
%V0
In triangle $ABC$, let $J$ be the center of the excircle tangent to side $BC$ at $A_{1}$ and to the extensions of the sides $AC$ and $AB$ at $B_{1}$ and $C_{1}$ respectively. Suppose that the lines $A_{1}B_{1}$ and $AB$ are perpendicular and intersect at $D$. Let $E$ be the foot of the perpendicular from $C_{1}$ to line $DJ$. Determine the angles $\angle{BEA_{1}}$ and $\angle{AEB_{1}}$.
Izvor: Međunarodna matematička olimpijada, shortlist 2006
Školjka 
, let 
be the center of the excircle tangent to side 
at 
and to the extensions of the sides 
and 
at 
and 
respectively. Suppose that the lines 
and 
. Let 
be the foot of the perpendicular from 
. Determine the angles 
and 
.