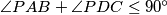
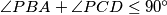
Let be a convex quadrilateral. A circle passing through the points and and a circle passing through the points and are externally tangent at a point inside the quadrilateral. Suppose that and . Prove that .
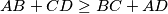
%V0
Let $ABCD$ be a convex quadrilateral. A circle passing through the points $A$ and $D$ and a circle passing through the points $B$ and $C$ are externally tangent at a point $P$ inside the quadrilateral. Suppose that $\angle{PAB}+\angle{PDC}\leq 90^\circ$ and $\angle{PBA}+\angle{PCD}\leq 90^\circ$.
Prove that $AB+CD \geq BC+AD$.
Izvor: Međunarodna matematička olimpijada, shortlist 2006
Školjka 
be a convex quadrilateral. A circle passing through the points 
and 
and a circle passing through the points 
and 
are externally tangent at a point 
inside the quadrilateral. Suppose that 
and 
. 
.