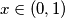
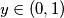
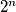
For let be the number whose -th digit after the decimal point is the -th digit after the decimal point of . Show that if is rational then so is .
%V0
For $x \in (0, 1)$ let $y \in (0, 1)$ be the number whose $n$-th digit after the decimal point is the $2^{n}$-th digit after the decimal point of $x$. Show that if $x$ is rational then so is $y$.
Izvor: Međunarodna matematička olimpijada, shortlist 2006
Školjka 
let 
be the number whose 
-th digit after the decimal point is the 
-th digit after the decimal point of 
. Show that if 
.