IMO Shortlist 2006 problem N3
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,5 We define a sequence 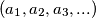 by setting
by setting
![a_{n} = \frac {1}{n}\left(\left[\frac {n}{1}\right] + \left[\frac {n}{2}\right] + \cdots + \left[\frac {n}{n}\right]\right)](/media/m/0/f/c/0fcd7236589e4454f518b8d8aa9fe147.png)
for every positive integer . Hereby, for every real
. Hereby, for every real  , we denote by
, we denote by ![\left[x\right]](/media/m/3/6/9/3697c66f8530757a1166f24a1fd325e6.png) the integral part of
the integral part of  (this is the greatest integer which is
(this is the greatest integer which is 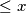 ).
).
a) Prove that there is an infinite number of positive integers such that
such that 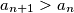 .
.
b) Prove that there is an infinite number of positive integers such that
such that 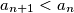 .
.
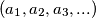 by setting
by setting ![a_{n} = \frac {1}{n}\left(\left[\frac {n}{1}\right] + \left[\frac {n}{2}\right] + \cdots + \left[\frac {n}{n}\right]\right)](/media/m/0/f/c/0fcd7236589e4454f518b8d8aa9fe147.png)
for every positive integer
 . Hereby, for every real
. Hereby, for every real  , we denote by
, we denote by ![\left[x\right]](/media/m/3/6/9/3697c66f8530757a1166f24a1fd325e6.png) the integral part of
the integral part of  (this is the greatest integer which is
(this is the greatest integer which is 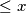 ).
). a) Prove that there is an infinite number of positive integers
 such that
such that 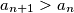 .
. b) Prove that there is an infinite number of positive integers
 such that
such that 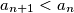 .
. Izvor: Međunarodna matematička olimpijada, shortlist 2006
 Školjka
Školjka 
