IMO Shortlist 2006 problem N6
Dodao/la:
arhiva2. travnja 2012. Let
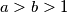
be relatively prime positive integers. Define the weight of an integer

, denoted by
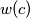
to be the minimal possible value of
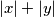
taken over all pairs of integers

and
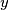
such that
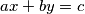
. An integer

is called a local champion if
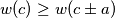
and
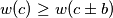
. Find all local champions and determine their number.
%V0
Let $a > b > 1$ be relatively prime positive integers. Define the weight of an integer $c$, denoted by $w(c)$ to be the minimal possible value of $|x| + |y|$ taken over all pairs of integers $x$ and $y$ such that $ax + by = c$. An integer $c$ is called a local champion if $w(c) \geq w(c \pm a)$ and $w(c) \geq w(c \pm b)$. Find all local champions and determine their number.
Izvor: Međunarodna matematička olimpijada, shortlist 2006