IMO Shortlist 2007 problem C2
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0 A rectangle  is partitioned in several (
is partitioned in several (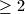 ) rectangles with sides parallel to those of
) rectangles with sides parallel to those of  . Given that any line parallel to one of the sides of
. Given that any line parallel to one of the sides of  , and having common points with the interior of
, and having common points with the interior of  , also has common interior points with the interior of at least one rectangle of the partition; prove that there is at least one rectangle of the partition having no common points with
, also has common interior points with the interior of at least one rectangle of the partition; prove that there is at least one rectangle of the partition having no common points with  's boundary.
's boundary.
Author: unknown author, Japan
 is partitioned in several (
is partitioned in several (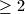 ) rectangles with sides parallel to those of
) rectangles with sides parallel to those of  . Given that any line parallel to one of the sides of
. Given that any line parallel to one of the sides of  , and having common points with the interior of
, and having common points with the interior of  , also has common interior points with the interior of at least one rectangle of the partition; prove that there is at least one rectangle of the partition having no common points with
, also has common interior points with the interior of at least one rectangle of the partition; prove that there is at least one rectangle of the partition having no common points with  's boundary.
's boundary. Author: unknown author, Japan
Izvor: Međunarodna matematička olimpijada, shortlist 2007
 Školjka
Školjka 
