IMO Shortlist 2007 problem C7
Dodao/la:
arhiva2. travnja 2012. Let
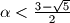
be a positive real number. Prove that there exist positive integers

and
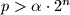
for which one can select
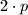
pairwise distinct subsets
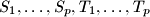
of the set
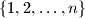
such that
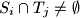
for all
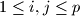
Author: Gerhard Wöginger, Austria
%V0
Let $\alpha < \frac {3 - \sqrt {5}}{2}$ be a positive real number. Prove that there exist positive integers $n$ and $p > \alpha \cdot 2^n$ for which one can select $2 \cdot p$ pairwise distinct subsets $S_1, \ldots, S_p, T_1, \ldots, T_p$ of the set $\{1,2, \ldots, n\}$ such that $S_i \cap T_j \neq \emptyset$ for all $1 \leq i,j \leq p$
Author: Gerhard Wöginger, Austria
Izvor: Međunarodna matematička olimpijada, shortlist 2007