IMO Shortlist 2007 problem C8
Given is a convex polygon
with
vertices. Triangle whose vertices lie on vertices of
is called good if all its sides are equal in length. Prove that there are at most
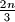
good triangles.
Author: unknown author, Ukraine
%V0
Given is a convex polygon $P$ with $n$ vertices. Triangle whose vertices lie on vertices of $P$ is called good if all its sides are equal in length. Prove that there are at most $\frac {2n}{3}$ good triangles.
Author: unknown author, Ukraine
Source: Međunarodna matematička olimpijada, shortlist 2007
Školjka 
