IMO Shortlist 2007 problem G3
Dodao/la:
arhiva2. travnja 2012. The diagonals of a trapezoid

intersect at point

. Point

lies between the parallel lines

and
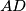
such that
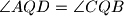
, and line

separates points

and

. Prove that
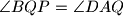
.
Author: unknown author, Ukraine
%V0
The diagonals of a trapezoid $ABCD$ intersect at point $P$. Point $Q$ lies between the parallel lines $BC$ and $AD$ such that $\angle AQD = \angle CQB$, and line $CD$ separates points $P$ and $Q$. Prove that $\angle BQP = \angle DAQ$.
Author: unknown author, Ukraine
Izvor: Međunarodna matematička olimpijada, shortlist 2007