IMO Shortlist 2007 problem G5
Kvaliteta:
Avg: 0,0Težina:
Avg: 8,0 Let  be a fixed triangle, and let
be a fixed triangle, and let  ,
,  ,
,  be the midpoints of sides
be the midpoints of sides  ,
,  ,
,  , respectively. Let
, respectively. Let  be a variable point on the circumcircle. Let lines
be a variable point on the circumcircle. Let lines 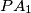 ,
, 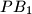 ,
, 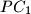 meet the circumcircle again at
meet the circumcircle again at 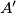 ,
, 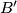 ,
, 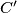 , respectively. Assume that the points
, respectively. Assume that the points  ,
,  ,
,  ,
, 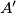 ,
, 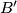 ,
, 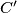 are distinct, and lines
are distinct, and lines 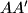 ,
, 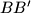 ,
, 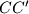 form a triangle. Prove that the area of this triangle does not depend on
form a triangle. Prove that the area of this triangle does not depend on  .
.
Author: Christopher Bradley, United Kingdom
 be a fixed triangle, and let
be a fixed triangle, and let  ,
,  ,
,  be the midpoints of sides
be the midpoints of sides  ,
,  ,
,  , respectively. Let
, respectively. Let  be a variable point on the circumcircle. Let lines
be a variable point on the circumcircle. Let lines 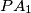 ,
, 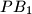 ,
, 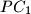 meet the circumcircle again at
meet the circumcircle again at 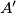 ,
, 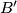 ,
, 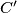 , respectively. Assume that the points
, respectively. Assume that the points  ,
,  ,
,  ,
, 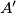 ,
, 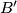 ,
, 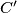 are distinct, and lines
are distinct, and lines 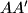 ,
, 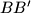 ,
, 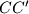 form a triangle. Prove that the area of this triangle does not depend on
form a triangle. Prove that the area of this triangle does not depend on  .
. Author: Christopher Bradley, United Kingdom
Izvor: Međunarodna matematička olimpijada, shortlist 2007
 Školjka
Školjka 
