IMO Shortlist 2007 problem G7
Dodao/la:
arhiva2. travnja 2012. Given an acute triangle

with
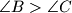
. Point

is the incenter, and

the circumradius. Point

is the foot of the altitude from vertex

. Point

lies on line

such that
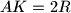
, and

separates

and

. Lines
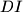
and
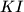
meet sides

and

at
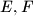
respectively. Let
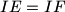
.
Prove that
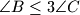
.
Author: Davoud Vakili, Iran
%V0
Given an acute triangle $ABC$ with $\angle B > \angle C$. Point $I$ is the incenter, and $R$ the circumradius. Point $D$ is the foot of the altitude from vertex $A$. Point $K$ lies on line $AD$ such that $AK = 2R$, and $D$ separates $A$ and $K$. Lines $DI$ and $KI$ meet sides $AC$ and $BC$ at $E,F$ respectively. Let $IE = IF$.
Prove that $\angle B\leq 3\angle C$.
Author: Davoud Vakili, Iran
Izvor: Međunarodna matematička olimpijada, shortlist 2007