IMO Shortlist 2007 problem G8
Kvaliteta:
Avg: 4,0Težina:
Avg: 9,0 Point  lies on side
lies on side  of a convex quadrilateral
of a convex quadrilateral  . Let
. Let  be the incircle of triangle
be the incircle of triangle 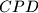 , and let
, and let  be its incenter. Suppose that
be its incenter. Suppose that  is tangent to the incircles of triangles
is tangent to the incircles of triangles 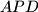 and
and 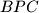 at points
at points  and
and  , respectively. Let lines
, respectively. Let lines  and
and  meet at
meet at  , and let lines
, and let lines 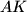 and
and 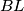 meet at
meet at  . Prove that points
. Prove that points  ,
,  , and
, and  are collinear.
are collinear.
Author: Waldemar Pompe, Poland
 lies on side
lies on side  of a convex quadrilateral
of a convex quadrilateral  . Let
. Let  be the incircle of triangle
be the incircle of triangle 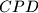 , and let
, and let  be its incenter. Suppose that
be its incenter. Suppose that  is tangent to the incircles of triangles
is tangent to the incircles of triangles 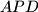 and
and 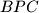 at points
at points  and
and  , respectively. Let lines
, respectively. Let lines  and
and  meet at
meet at  , and let lines
, and let lines 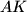 and
and 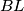 meet at
meet at  . Prove that points
. Prove that points  ,
,  , and
, and  are collinear.
are collinear. Author: Waldemar Pompe, Poland
Izvor: Međunarodna matematička olimpijada, shortlist 2007
 Školjka
Školjka 
