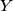
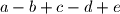
Let be a set of 10,000 integers, none of them is divisible by 47. Prove that there exists a 2007-element subset of such that is not divisible by 47 for any
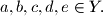
Author: Gerhard Wöginger, Netherlands
%V0
Let $X$ be a set of 10,000 integers, none of them is divisible by 47. Prove that there exists a 2007-element subset $Y$ of $X$ such that $a - b + c - d + e$ is not divisible by 47 for any $a,b,c,d,e \in Y.$
Author: Gerhard Wöginger, Netherlands
Izvor: Međunarodna matematička olimpijada, shortlist 2007
Školjka 
be a set of 10,000 integers, none of them is divisible by 47. Prove that there exists a 2007-element subset 
of 
is not divisible by 47 for any 