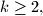
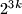
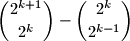
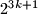
For every integer prove that divides the number but does not.
Author: unknown author, Poland
%V0
For every integer $k \geq 2,$ prove that $2^{3k}$ divides the number
$$\binom{2^{k + 1}}{2^{k}} - \binom{2^{k}}{2^{k - 1}}$$
but $2^{3k + 1}$ does not.
Author: unknown author, Poland
Izvor: Međunarodna matematička olimpijada, shortlist 2007
Školjka 
prove that 
divides the number 
does not.