IMO Shortlist 2007 problem N5
Dodao/la:
arhiva2. travnja 2012. Find all surjective functions
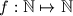
such that for every
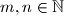
and every prime
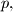
the number
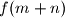
is divisible by

if and only if
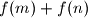
is divisible by
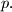
Author: Mohsen Jamaali and Nima Ahmadi Pour Anari, Iran
%V0
Find all surjective functions $f: \mathbb{N} \mapsto \mathbb{N}$ such that for every $m,n \in \mathbb{N}$ and every prime $p,$ the number $f(m + n)$ is divisible by $p$ if and only if $f(m) + f(n)$ is divisible by $p.$
Author: Mohsen Jamaali and Nima Ahmadi Pour Anari, Iran
Izvor: Međunarodna matematička olimpijada, shortlist 2007