IMO Shortlist 2007 problem N7
Dodao/la:
arhiva2. travnja 2012. For a prime

and a given integer

let
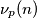
denote the exponent of

in the prime factorisation of
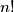
. Given
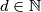
and
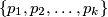
a set of

primes, show that there are infinitely many positive integers

such that
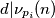
for all
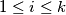
.
Author: Tejaswi Navilarekkallu, India
%V0
For a prime $p$ and a given integer $n$ let $\nu_p(n)$ denote the exponent of $p$ in the prime factorisation of $n!$. Given $d \in \mathbb{N}$ and $\{p_1,p_2,\ldots,p_k\}$ a set of $k$ primes, show that there are infinitely many positive integers $n$ such that $d|\nu_{p_i}(n)$ for all $1 \leq i \leq k$.
Author: Tejaswi Navilarekkallu, India
Izvor: Međunarodna matematička olimpijada, shortlist 2007