IMO Shortlist 2008 problem A3
Kvaliteta:
Avg: 3,0Težina:
Avg: 7,0 Let 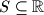 be a set of real numbers. We say that a pair
be a set of real numbers. We say that a pair 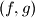 of functions from
of functions from  into
into  is a Spanish Couple on
is a Spanish Couple on  , if they satisfy the following conditions:
, if they satisfy the following conditions:
(i) Both functions are strictly increasing, i.e.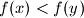 and
and 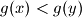 for all
for all  ,
, 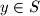 with
with 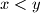 ;
;
(ii) The inequality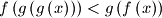 holds for all
holds for all 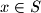 .
.
Decide whether there exists a Spanish Couple on the set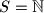 of positive integers; on the set
of positive integers; on the set 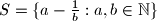
Proposed by Hans Zantema, Netherlands
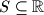 be a set of real numbers. We say that a pair
be a set of real numbers. We say that a pair 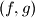 of functions from
of functions from  into
into  is a Spanish Couple on
is a Spanish Couple on  , if they satisfy the following conditions:
, if they satisfy the following conditions: (i) Both functions are strictly increasing, i.e.
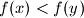 and
and 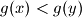 for all
for all  ,
, 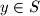 with
with 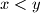 ;
; (ii) The inequality
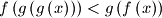 holds for all
holds for all 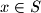 .
. Decide whether there exists a Spanish Couple on the set
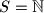 of positive integers; on the set
of positive integers; on the set 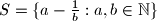
Proposed by Hans Zantema, Netherlands
Izvor: Međunarodna matematička olimpijada, shortlist 2008
 Školjka
Školjka 
