IMO Shortlist 2008 problem A5
Dodao/la:
arhiva2. travnja 2012. Let

,

,

,

be positive real numbers such that
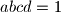
and
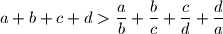
. Prove that
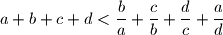
Proposed by Pavel Novotný, Slovakia
%V0
Let $a$, $b$, $c$, $d$ be positive real numbers such that $abcd = 1$ and $a + b + c + d > \dfrac{a}{b} + \dfrac{b}{c} + \dfrac{c}{d} + \dfrac{d}{a}$. Prove that
$$a + b + c + d < \dfrac{b}{a} + \dfrac{c}{b} + \dfrac{d}{c} + \dfrac{a}{d}$$
Proposed by Pavel Novotný, Slovakia
Izvor: Međunarodna matematička olimpijada, shortlist 2008