IMO Shortlist 2008 problem A6
Dodao/la:
arhiva2. travnja 2012. Let
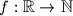
be a function which satisfies
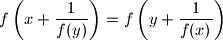
for all

,
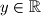
. Prove that there is a positive integer which is not a value of

.
Proposed by Žymantas Darbėnas (Zymantas Darbenas), Lithania
%V0
Let $f: \mathbb{R}\to\mathbb{N}$ be a function which satisfies $f\left(x + \dfrac{1}{f(y)}\right) = f\left(y + \dfrac{1}{f(x)}\right)$ for all $x$, $y\in\mathbb{R}$. Prove that there is a positive integer which is not a value of $f$.
Proposed by Žymantas Darbėnas (Zymantas Darbenas), Lithania
Izvor: Međunarodna matematička olimpijada, shortlist 2008