For
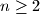
, let

,
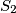
,

,
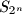
be
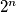
subsets of
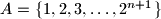
that satisfy the following property: There do not exist indices

and

with
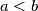
and elements

,

,
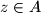
with
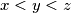
and

,
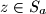
, and

,
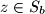
. Prove that at least one of the sets

,
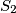
,

,
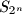
contains no more than
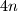
elements.
Proposed by Gerhard Woeginger, Netherlands
%V0
For $n\ge 2$, let $S_1$, $S_2$, $\ldots$, $S_{2^n}$ be $2^n$ subsets of $A = \{1, 2, 3, \ldots, 2^{n + 1}\}$ that satisfy the following property: There do not exist indices $a$ and $b$ with $a < b$ and elements $x$, $y$, $z\in A$ with $x < y < z$ and $y$, $z\in S_a$, and $x$, $z\in S_b$. Prove that at least one of the sets $S_1$, $S_2$, $\ldots$, $S_{2^n}$ contains no more than $4n$ elements.
Proposed by Gerhard Woeginger, Netherlands