IMO Shortlist 2008 problem G3
Dodao/la:
arhiva2. travnja 2012. Let

be a convex quadrilateral and let

and

be points in

such that
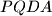
and
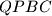
are cyclic quadrilaterals. Suppose that there exists a point

on the line segment

such that
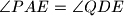
and
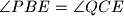
. Show that the quadrilateral

is cyclic.
Proposed by John Cuya, Peru
%V0
Let $ABCD$ be a convex quadrilateral and let $P$ and $Q$ be points in $ABCD$ such that $PQDA$ and $QPBC$ are cyclic quadrilaterals. Suppose that there exists a point $E$ on the line segment $PQ$ such that $\angle PAE = \angle QDE$ and $\angle PBE = \angle QCE$. Show that the quadrilateral $ABCD$ is cyclic.
Proposed by John Cuya, Peru
Izvor: Međunarodna matematička olimpijada, shortlist 2008