IMO Shortlist 2008 problem N1
Dodao/la:
arhiva2. travnja 2012. Let

be a positive integer and let

be a prime number. Prove that if

,

,

are integers (not necessarily positive) satisfying the equations
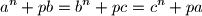
then
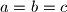
.
Proposed by Angelo Di Pasquale, Australia
%V0
Let $n$ be a positive integer and let $p$ be a prime number. Prove that if $a$, $b$, $c$ are integers (not necessarily positive) satisfying the equations
$$a^n + pb = b^n + pc = c^n + pa$$
then $a = b = c$.
Proposed by Angelo Di Pasquale, Australia
Izvor: Međunarodna matematička olimpijada, shortlist 2008