IMO Shortlist 2008 problem N5
Dodao/la:
arhiva2. travnja 2012. For every
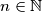
let
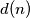
denote the number of (positive) divisors of

. Find all functions
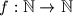
with the following properties:
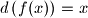
for all
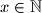
.
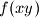
divides
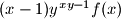
for all

,
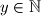
.
Proposed by Bruno Le Floch, France
%V0
For every $n\in\mathbb{N}$ let $d(n)$ denote the number of (positive) divisors of $n$. Find all functions $f: \mathbb{N}\to\mathbb{N}$ with the following properties: $d\left(f(x)\right) = x$ for all $x\in\mathbb{N}$. $f(xy)$ divides $(x - 1)y^{xy - 1}f(x)$ for all $x$, $y\in\mathbb{N}$.
Proposed by Bruno Le Floch, France
Izvor: Međunarodna matematička olimpijada, shortlist 2008