IMO Shortlist 2009 problem A1
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0 Find the largest possible integer  , such that the following statement is true:
, such that the following statement is true:
Let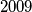 arbitrary non-degenerated triangles be given. In every triangle the three sides are coloured, such that one is blue, one is red and one is white. Now, for every colour separately, let us sort the lengths of the sides. We obtain
arbitrary non-degenerated triangles be given. In every triangle the three sides are coloured, such that one is blue, one is red and one is white. Now, for every colour separately, let us sort the lengths of the sides. We obtain
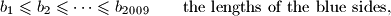

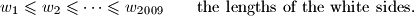
Then there exist indices
indices  such that we can form a non-degenerated triangle with side lengths
such that we can form a non-degenerated triangle with side lengths 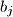 ,
, 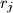 ,
, 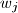 .
.
Proposed by Michal Rolinek, Czech Republic
 , such that the following statement is true:
, such that the following statement is true: Let
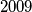 arbitrary non-degenerated triangles be given. In every triangle the three sides are coloured, such that one is blue, one is red and one is white. Now, for every colour separately, let us sort the lengths of the sides. We obtain
arbitrary non-degenerated triangles be given. In every triangle the three sides are coloured, such that one is blue, one is red and one is white. Now, for every colour separately, let us sort the lengths of the sides. We obtain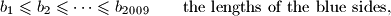

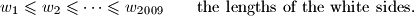
Then there exist
 indices
indices  such that we can form a non-degenerated triangle with side lengths
such that we can form a non-degenerated triangle with side lengths 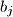 ,
, 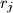 ,
, 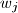 .
.Proposed by Michal Rolinek, Czech Republic
Izvor: Međunarodna matematička olimpijada, shortlist 2009
 Školjka
Školjka 
